কন্টেন্ট

• পদক্ষেপ
• পদ্ধতি 1 এর 1: ব্যাসার্ধ সূত্র ব্যবহার
• 3 এর পদ্ধতি 2: মূল ধারণাগুলি সংজ্ঞায়িত করুন
• পদ্ধতি 3 এর 3: দুটি পয়েন্টের মধ্যে দূরত্ব হিসাবে ব্যাসার্ধটি সন্ধান করা
• পরামর্শ

একটি গোলকের ব্যাসার্ধ (পরিবর্তনশীল হিসাবে সংক্ষেপে) r বা আর।) গোলকের ঠিক কেন্দ্র থেকে সেই গোলকের পৃষ্ঠের বিন্দুতে দূরত্ব। বৃত্তের মতো, গোলকের ব্যাসার্ধ, পরিধি, ক্ষেত্র এবং ক্ষেত্রের আয়তন গণনার জন্য প্রায়শই একটি গোলকের ব্যাসার্ধ তবে, আপনি গোলকের ব্যাসার্ধ খুঁজতে ব্যাস, পরিধি ইত্যাদি থেকে পিছনেও কাজ করতে পারেন। আপনার কাছে থাকা ডেটার জন্য উপযুক্ত সূত্রটি ব্যবহার করুন।

পদক্ষেপ

পদ্ধতি 1 এর 1: ব্যাসার্ধ সূত্র ব্যবহার

1. ব্যাসটি জানা থাকলে ব্যাসার্ধ নির্ধারণ করুন। ব্যাসার্ধটি আধ ব্যাসের, তাই আপনি সূত্রটি ব্যবহার করুন r = D / 2। এটি একটি বৃত্তের ব্যাসার্ধের ব্যাসার্ধ গণনা করার পদ্ধতির সাথে সমান।
   • যদি আপনার 16 সেন্টিমিটার ব্যাসের সাথে একটি গোলক থাকে, আপনি 16/2 = দিয়ে ব্যাসার্ধ গণনা করুন 8 সেমি। ব্যাস যদি 42 হয় তবে ব্যাসার্ধটি হয় 21.
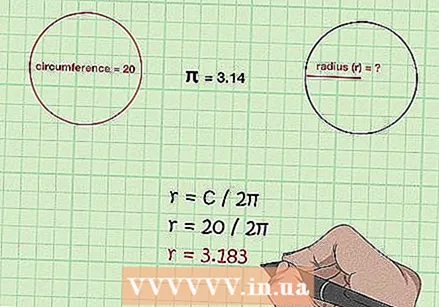2. পরিধিটি জানা থাকলে ব্যাসার্ধ নির্ধারণ করুন। সূত্রটি ব্যবহার করুন সি / 2π। পরিধিটি ডিডের সমান হওয়ায় যেগুলি ঘুরতে 2πr এর সমান হয়, পরিধিটি 2π দ্বারা ভাগ করে ব্যাসার্ধ গণনা করে π
   • আপনার যদি 20 মিটার পরিধি নিয়ে একটি গোলক থাকে তবে আপনি ব্যাসার্ধটি খুঁজে পাবেন 20 / 2π = 3.183 মি.
   • ব্যাসার্ধ এবং একটি বৃত্তের পরিধিগুলির মধ্যে রূপান্তর করতে আপনি একই সূত্রটি ব্যবহার করতে পারেন।
3. গোলকের পরিমাণের পরিমাণ জানলে ব্যাসার্ধ গণনা করুন। সূত্রটি (V / V) (3/4) ব্যবহার করুন) একটি গোলকের ভলিউম ভি = (4/3) এর সমীকরণ থেকে প্রাপ্ত। আর এর সমীকরণটি সমাধান করে আপনি ((ভি / π) (3/4)) = আর পেয়েছেন, সুতরাং এটি স্পষ্ট হয়ে যায় যে একটি বা গোলকের ব্যাসার্ধ π, বার 3/4 দ্বারা ভাগ করে ভলিউমের সমান হয় 1/3 পাওয়ার (বা কিউব রুট)।
   • যদি আপনার 100 সেন্টিমিটার আয়তনের একটি গোলক থাকে তবে আপনি ব্যাসার্ধটি নীচে পাবেন:
     • ((ভি / π) (3/4)) = আর
     • ((100 / π) (3/4)) = আর
     • ((31.83) (3/4)) = আর
     • (23.87) = আর
     • 2,88 = আর
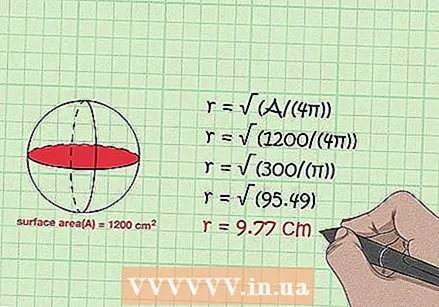4. পৃষ্ঠের ব্যাসার্ধ নির্ধারণ করুন। সূত্রটি ব্যবহার করুন আর = √ (এ / (৪π))। আপনি A = 4πr সমীকরণের সাথে একটি গোলকের ক্ষেত্রফল গণনা করুন। R এর সমীকরণটি সমাধান করা √ (এ / (4π)) = আর দেয়, যার অর্থ হল একটি গোলকের ব্যাসার্ধটি 4 area দ্বারা বিভক্ত তার ক্ষেত্রের বর্গমূলের সমান π আপনি একই ফলাফলের জন্য (এ / (4π)) থেকে 1/2 এ পাওয়ারও করতে পারেন।
   • আপনার যদি 1200 সেন্টিমিটারের ক্ষেত্র সহ গোলকটি থাকে তবে আপনি ব্যাসার্ধটি নীচের হিসাবে গণনা করুন:
     • √ (এ / (৪π)) = আর
     • 12 (1200 / (4π)) = আর
     • √ (300 / (π)) = আর
     • 95 (95.49) = আর
     • 9.77 সেমি = আর

3 এর পদ্ধতি 2: মূল ধারণাগুলি সংজ্ঞায়িত করুন

1. একটি গোলকের প্রাথমিক মাত্রাগুলি জানুন। ব্যাসার্ধ (r) গোলকের ঠিক কেন্দ্র থেকে গোলকের পৃষ্ঠের যে কোনও বিন্দুর দূরত্ব। সাধারণভাবে, আপনি যদি কোনও গোলকের ব্যাসার্ধ, পরিধি, আয়তন বা অঞ্চল জানেন তবে আপনি কোনও গোলকের ব্যাসার্ধটি সন্ধান করতে পারেন।
   • ব্যাস (ডি): একটি গোলকের কেন্দ্রের মধ্য দিয়ে রেখার দৈর্ঘ্য & ndash; ব্যাসার্ধ দ্বিগুণ ব্যাসটি গোলকের কেন্দ্রের মধ্য দিয়ে একটি রেখার দৈর্ঘ্য, গোলকের বাইরের এক বিন্দু থেকে সরাসরি এর বিপরীতে সম্পর্কিত বিন্দুতে। অন্য কথায়, গোলকের দুটি পয়েন্টের মধ্যে সর্বাধিক সম্ভাব্য দূরত্ব।
   • পরিবেশন (সি): এর প্রশস্ত বিন্দুতে গোলকের চারপাশে এক-মাত্রিক দূরত্ব। অন্য কথায়, একটি গোলকের বৃত্তাকার ক্রস-বিভাগের পরিধি, যার বিমানটি গোলকের কেন্দ্রস্থল দিয়ে চলে runs
   • খণ্ড (V): গোলকের মধ্যে ত্রি-মাত্রিক স্থান। এটি "গোলকের অধীনে স্থান"।
   • পৃষ্ঠ (ক): গোলকের বাইরের পৃষ্ঠের দ্বিমাত্রিক স্থান। গোলকের বাইরের অংশটি জুড়ে সমতল স্থানের পরিমাণ।
   • পাই (π): বৃত্তের ব্যাসের সাথে বৃত্তের পরিধির অনুপাতকে প্রকাশ করা একটি ধ্রুবক। পাই এর প্রথম 10 সংখ্যা সর্বদা থাকে 3,141592653যদিও এটি সাধারণত গোল হয় round 3,14.
2. ব্যাসার্ধ নির্ধারণ করতে বিভিন্ন পরিমাপ ব্যবহার করুন। আপনি একটি গোলকের ব্যাসার্ধ গণনা করতে ব্যাস, পরিধি, আয়তন এবং ক্ষেত্র ব্যবহার করতে পারেন। যদি আপনি ব্যাসার্ধের দৈর্ঘ্য জানেন তবে আপনি এই সংখ্যার যে কোনওটি গণনা করতে পারেন। সুতরাং, ব্যাসার্ধটি খুঁজতে, আপনি এই অংশগুলি গণনা করার সূত্রগুলি বিপরীত করতে পারেন। ব্যাস, পরিধি, ক্ষেত্র এবং ভলিউম গণনা করতে ব্যাসার্ধের সূত্রগুলি শিখুন।
   • ডি = 2 আর। বৃত্তগুলির মতো, একটি গোলকের ব্যাসার্ধের দ্বিগুণ।
   • সি = πD বা 2πr। চেনাশোনাগুলির মতো, একটি গোলকের পরিধি তার ব্যাসের দ্বিগুণ। ব্যাসটি ব্যাসার্ধের দ্বিগুণ হওয়ার কারণে আমরা এটিও বলতে পারি যে পরিধিটি ব্যাসার্ধের দ্বিগুণ π
   • ভি = (4/3) আর। একটি গোলকের আয়তন ব্যাসার্ধ থেকে কিউবিক পাওয়ার (r x r x r), গুণমান π, গুণ 4/3।
   • এ = 4πr। একটি গোলকের ক্ষেত্রফল দুটি (আরএক্সআর) গুণমানের বার ব্যাসার্ধের ব্যাসার্ধ হয় 4 বার যেহেতু একটি বৃত্তের পরিধি πr হয় তাই এটিও বলা যেতে পারে যে একটি গোলকের ক্ষেত্রফল চারটি সমান তার বৃত্তের ক্ষেত্রফল দ্বারা গঠিত বৃত্তের ক্ষেত্রফলকে।

পদ্ধতি 3 এর 3: দুটি পয়েন্টের মধ্যে দূরত্ব হিসাবে ব্যাসার্ধটি সন্ধান করা

1. গোলকের কেন্দ্রের স্থানাঙ্ক (x, y, z) সন্ধান করুন। গোলকের ব্যাসার্ধ সম্পর্কে চিন্তা করার এক উপায় হল গোলকের কেন্দ্র এবং তার পৃষ্ঠের যে কোনও বিন্দুর মধ্যবর্তী দূরত্ব। যেহেতু এটি সত্য, আপনি আদর্শ দূরত্বের সূত্রের বৈচিত্রটি ব্যবহার করে দুটি পয়েন্টের মধ্যে দূরত্ব গণনা করে গোলকের ব্যাসার্ধ নির্ধারণ করতে কেন্দ্রের স্থানাঙ্ক এবং গোলকের পৃষ্ঠের একটি বিন্দু ব্যবহার করতে পারেন। শুরু করতে, গোলকের কেন্দ্রের স্থানাঙ্কগুলি সন্ধান করুন। লক্ষ্য করুন যে একটি গোলকটি ত্রিমাত্রিক, এটি কোনও (x, y) জয়েন্টের পরিবর্তে একটি (x, y, z) পয়েন্ট হবে।
   • এটি উদাহরণ সহ বোঝা সহজ। ধরুন কেন্দ্র হিসাবে একটি গোলক দেওয়া হয়েছে (-1, 4, 12)। পরবর্তী কয়েকটি পদক্ষেপে, আমরা ব্যাসার্ধ নির্ধারণে এই পয়েন্টটি ব্যবহার করতে যাচ্ছি।
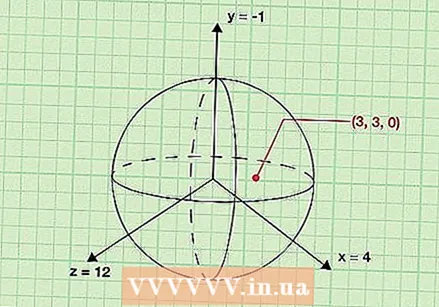2. গোলকের পৃষ্ঠের পৃষ্ঠের বিন্দুর স্থানাঙ্কগুলি সন্ধান করুন। তারপরে আপনাকে গোলকের পৃষ্ঠের কোনও বিন্দুর (x, y, z) স্থানাঙ্ক নির্ধারণ করতে হবে। এটা সম্ভব প্রতিটি গোলকের পৃষ্ঠের দিকে নির্দেশ করুন। কারণ সংজ্ঞা অনুসারে গোলকের পৃষ্ঠের সমস্ত পয়েন্টগুলি কেন্দ্র থেকে সমান সমান, আপনি ব্যাসার্ধ নির্ধারণ করতে যে কোনও পয়েন্ট ব্যবহার করতে পারেন।
   • আমাদের উদাহরণ অনুশীলনের প্রসঙ্গে আমরা সেই বিষয়টিকে তৈরি করি (3, 3, 0) গোলকের পৃষ্ঠতল। এই বিন্দু এবং কেন্দ্রের মধ্যবর্তী দূরত্ব গণনা করে আমরা ব্যাসার্ধটি আবিষ্কার করতে পারি।
3. D = √ (সূত্র) সূত্র দিয়ে ব্যাসার্ধ নির্ধারণ করুন₂ - এক্স₁) + (y)₂ - y₁) + (জেড)₂ - জেড₁)). আপনি যখন গোলকের কেন্দ্র এবং গোলকের পৃষ্ঠের একটি বিন্দু জানেন তবে আপনি তাদের মধ্যকার দূরত্ব গণনা করে ব্যাসার্ধটি আবিষ্কার করতে পারেন। ত্রি-মাত্রিক দূরত্বের সূত্রটি d = √ (x) ব্যবহার করুন₂ - এক্স₁) + (y)₂ - y₁) + (জেড)₂ - জেড₁)), যেখানে d দূরত্ব, (x₁, y₁, জেড₁) কেন্দ্রের স্থানাঙ্কগুলি এবং (এক্স) উপস্থাপন করে₂, y₂, জেড₂) দুটি পয়েন্টের মধ্যে দূরত্ব নির্ধারণের জন্য পৃষ্ঠের পয়েন্টের স্থানাঙ্ককে উপস্থাপন করে।
   • আমাদের উদাহরণস্বরূপ, আমরা (x, 4, -1, 12) এর বিকল্প করব₁, y₁, জেড₁) এবং (3, 3, 0) এর জন্য (x₂, y₂, জেড₂), নিম্নলিখিত হিসাবে এটি সমাধান:
     • d = √ ((এক্স₂ - এক্স₁) + (y)₂ - y₁) + (জেড)₂ - জেড₁))
     • d = √ ((3 - 4) + (3 - -1) + (0 - 12))
     • d = √ ((- 1) + (4) + (-12)
     • d = √ (1 + 16 + 144)
     • d = √ (161)
     • d = 12.69। এটি আমাদের গোলকের ব্যাসার্ধ।
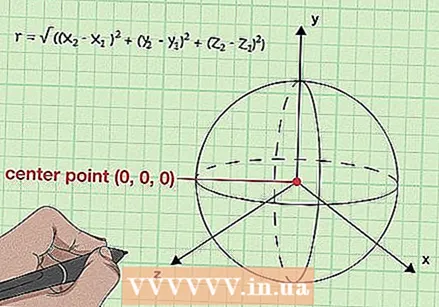4. সাধারণভাবে, জানতে হবে যে r = √ ((এক্স₂ - এক্স₁) + (y)₂ - y₁) + (জেড)₂ - জেড₁)). একটি গোলকের ক্ষেত্রে, পৃষ্ঠের প্রতিটি বিন্দুটির গোলকের কেন্দ্র থেকে একই দূরত্ব থাকে। উপরের ত্রিমাত্রিক দূরত্বের সূত্রটি গ্রহণ করে এবং ব্যাসার্ধ "d" এর পরিবর্তে ব্যাসার্ধের "r" ব্যাসার্ধের পরিবর্তে আমরা একটি সমীকরণ পাই যা আমাদের প্রদত্ত যে কোনও কেন্দ্র বিন্দুতে ব্যাসার্ধকে সন্ধান করতে দেয় (x₁, y₁, জেড₁) এবং পৃষ্ঠের কোনও সম্পর্কিত পয়েন্ট (x₂, y₂, জেড₂).
   • এই সমীকরণের উভয় দিককে স্কোয়ার করে আমরা পাই: r = (x₂ - এক্স₁) + (y)₂ - y₁) + (জেড)₂ - জেড₁)। দ্রষ্টব্য: এটি মূলত গোলকের (r = x + y + z) মানক সমীকরণের সমান, কেন্দ্রটি সমান (0,0,0) ধরে ধরে।

পরামর্শ

• অপারেশন ক্রম গুরুত্বপূর্ণ। আপনি যদি গণনা বিধি কীভাবে কাজ করে তা নিশ্চিত না হন এবং আপনার ক্যালকুলেটরটি প্রথম বন্ধনী সমর্থন করে তবে সেগুলি অবশ্যই ব্যবহার করবেন তা নিশ্চিত করুন।
• এই নিবন্ধটি তৈরি করা হয়েছিল কারণ এই বিষয়টির উচ্চ চাহিদা ছিল। তবে, আপনি যদি প্রথমবারের জন্য স্থানিক জ্যামিতিটি বোঝার চেষ্টা করছেন, তবে অন্য দিক দিয়ে শুরু করা ভাল: ব্যাসার্ধটি দেওয়া হলে একটি গোলকের বৈশিষ্ট্য গণনা করা।
• পাই বা হ'ল একটি গ্রীক অক্ষর যা তার বৃত্তের ব্যাসের অনুপাতকে তার পরিধি হিসাবে নির্দেশ করে। এটি একটি অযৌক্তিক সংখ্যা এবং বাস্তব সংখ্যার অনুপাত হিসাবে লেখা যায় না। অনেকগুলি আনুমানিকতা রয়েছে এবং ৩৩৩/১০6 পিআই চার দশমিক স্থানে ফিরে আসে। আজ বেশিরভাগ লোকেরা প্রায় 3.14 এর কথা মনে রাখে যা সাধারণত দৈনন্দিন প্রয়োজনের জন্য যথেষ্ট সঠিক accurate